|
Lezione Quinta a cura di Alessandro BELLOTTO pag. 1 | ||
|
|
Potenza necessaria al sostentamento dell’elicottero |
|
|
|
Per introdurre questo argomento bisogna fare una premessa, ovvero: tutta questa lezione ai fini della conoscenza vera e propria dell’elicottero come mezzo capace di volare, risulta esser quasi superflua e può interessare solamente un appassionato di meccanica, perciò la sua esposizione è puramente accademica. Come si può notare in (Fig.28) il rotore principale con la sua azione sposta una grande massa d’aria accelerandola dall’alto verso il basso ad una certa velocità, questo consente a se medesimo, per reazione, si spostarsi verso l’alto.
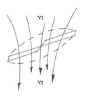
Fig. 28 La velocità media con cui l’aria attraversa il rotore nell’unità di tempo viene anche definita velocità indotta. Ora, per meglio comprendere l’entità della forza necessaria a muovere questa massa d’aria, svilupperemo la formula servendoci delle grandezze: (F
= m · a)
cioè a dire: Forza = massa per accelerazione da cui la (m = V · φ) cioè a dire: massa = Volume per densità per cui avremo che (F = V · φ · a) sappiamo
che il Volume (V = π · R² · v) cioè a dire:
Volume = pi-greco per Raggio² per velocità da ciò alla fine si ottiene che F = π · R² · v · φ · a cioè a dire: Volume = pi-greco per
Raggio² per velocità per densità per accelerazione e sappiamo
anche che l’accelerazione a
= (v2 – v1)² perciò avremo
che la F = π · R² · v
· φ · 2 Vi semplificando avremo F
= π · R² · Vi² · φ · 2 cioè a dire: Forza = pi-greco per Raggio² per velocitಠper densità per 2 tutta questa dimostrazione sta
semplicemente a indicare che la forza necessaria a muovere la massa d’aria
utile a creare la portanza, è direttamente proporzionale alla massa di aria
che le pale muovono accelerandola dall’alto verso il basso. Qualcuno si
chiederà perché R² semplicemente perché le pale che descrivono il cerchio
del rotore sono due.
|
|
